Masalah Steady State Sistem Kendali
Masalah Kesalahan Steady State
Kendali proporsional memiliki kelemahan / kekurangan yang mendasar yakni masalah kesalahan dalam keadaan steady state. Dalam penerapan pada sistim-sistim di lapangan, kendali proporsional tidak dapat mengatur variabel yang dikendalikan hingga mencapai keadaan dimana besarnya error adalah 0. Hal ini disebabkan karena pada saat pembebanan mendekati nilai kendali yang diinginkan, gaya koreksi yang dikerjakan turn mendekati nol, sehingga dengan gaya yang kecil ini, tidak dapat dilakukan kerja untuk mengatasi gaya gesek, beban akan berhenti pada posisi sebelum garis batas yang ditentukan.
Gaya gesek selalu ada pada sistim-sistim mekanis, gaya ini adalah suatu gaya non-linier yang bekerja melawan gaya yang diberikan kepada sistim. Dalam kenyataannya, beban tidak akan bergerak sama sekali hingga gaya gesekan dapat dilawan. Gambar 1.8(b) menunjukkan suatu model beban pegas sebagai contoh sistim kendali proporsional. Beban berada pada permukaan dengan gaya gesek pada bagian tengah dari suatu dudukan yang terhubung dengan dua pegas. Gambar 1.8(b) menunjukkan apa yang terjadi apaabila dudukan dengan cepat bergerak ke kanan. Pada awalnya, dorong dan tarikan yang diberikan oleh kedua pegas menggeser beban kekanan. Pada saat beban mendekati posisi tengahnya yang baru, gaya yang berkurang dari pegas-pegas dilawan oleh gaya gesek, dan beban akan berhenti sebelum mencapai posisi set point [Gambar 1.7(c)]. Kesalahan steady state adalah perbedaan jarak dimana beban berhenti dan posisi set point (posisi yang diinginkan). Daerah ini pada masing-masing sisi, dimana gaya pendorong tidak dapat dengan tepat menempatkan beban (menempatkan posisi / variabel yang dikendalikan) disebut sebagai daerah mati (dead zone) atau jalur mati (dead band). Faktor-faktor lainnya yang menyebabkan terjadinya daerah mati adalah hal-hal seperti, gerak balik bagian mekanis, pembengkokan bagian-bagian mekanik, dan rancangan pengendali yang buruk.
Contoh 1.2
Suatu sistim kendali posisi memiliki gain Kp sebesar 2 in. oz/deg dan dikerjakan melawan suatu torsi gesek konstan sebesar 6 in. oz. Berapa ukuran dari daerah mati yang terjadi?
Jawaban
Untuk melawan gaya gesek, sistim harus mengendalikan motor agar menghasilkan keluaran sebesar 6 in.oz. Disebabkan masuakn ke pengendali adalah sinyal kesalahan. Mkaka diperlukan untuk mencari nilai error / kesalahan yang dihasilkan oleh controller dengan output sebesar 6 in oz. Dengan menggunakan persamaan dasar (1.1)
![]()
Dengan mengubah persamaan ini sesuai kebutuhan,
![]()
Dengan error sebesar 3° pada masing-masing sisi, maka dead band adalah sebesar 6°.
Salah cara untuk mengurangi kesalahan steady state error adalah dengan meningkatkan gain dari sistim (dalam hal ini nilai KP pada persamaan 11.1), yang dapat dilakukan pada model sistim pada Gambar 11.8, dengan menggunakan pegas-pegas yang lebih kaku. Tinjau diagram pada Gambar 1.9. Gambar ini menunjukan gaya pembalik yang bekerja pada suatu beban dengan dua gain sistim masing-masing KPA dan KPB. Perhatikan bahwa dalam kedua kasus ini, besarnya gaya pembalik berbanding lurus (proporsional) dengan error yang terjadi. Gaya pembalik yang diperlukan untuk melawan gaya gesek ditunjukkan dengan garis putus-putus. Untuk sistim dengan gain yang lebih rendah, error yang terjadi akibat gaya gesek ditunjukkan sebagai EB. Untuk sistim dengan gain yang tinggi, tidak dibutuhkan untuk terjadinya defleksi yang besar dari posisi set point untuk menghasilkan gaya pembalik yang sesuai untuk melawan gaya gesek. Sistim ini memiliki tingkat steady state error yang lebih kecil, ditunjukan oleh EA. Kelihatan gain untuk semua sistim dapat dibuat sebesar mungkin; namun, nilai KP yang besar akan cenderung menyebabkan sistim menjadi tidak stabil (mengalami osilasi). Dengan demikian memperbesar gain tanpa batasan bukanlah suatu strategi kendali yang baik.
Dengan error sebesar 3° pada masing-masing sisi, maka dead band adalah sebesar 6°.
Salah satu cara untuk mengurangi kesalahan steady state error adalah dengan meningkatkan gain dari sistim (dalam hal ini nilai KP pada persamaan 1.1), yang dapat dilakukan pada model sistim pada Gambar 11.8, dengan menggunakan pegas-pegas yang lebih kaku. Tinjau diagram pada Gambar 1.9. Gambar ini menunjukan gaya pembalik yang bekerja pada suatu beban dengan dua gain sistim masing-masing KPA dan KPB. Perhatikan bahwa dalam kedua kasus ini, besarnya gaya pembalik berbanding lurus (proporsional) dengan error yang terjadi. Gaya pembalik yang diperlukan untuk melawan gaya gesek ditunjukkan dengan garis putus-putus. Untuk sistim dengan gain yang lebih rendah, error yang terjadi akibat gaya gesek ditunjukkan sebagai EB. Untuk sistim dengan gain yang tinggi, tidak dibutuhkan untuk terjadinya defleksi yang besar dari posisi set point untuk menghasilkan gaya pembalik yang sesuai untuk melawan gaya gesek. Sistim ini memiliki tingkat steady state error yang lebih kecil, ditunjukan oleh EA. Kelihatan gain untuk semua sistim dapat dibuat sebesar mungkin; namun, nilai KP yang besar akan cenderung menyebabkan sistim menjadi tidak stabil (mengalami osilasi). Dengan demikian memperbesar gain tanpa batasan bukanlah suatu strategi kendali yang baik.
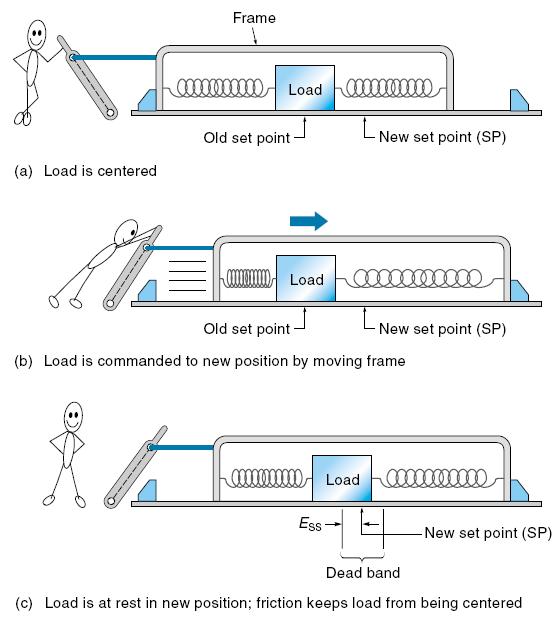
Gambar 1. 8. Gaya gesek menyebabkan terjadinya kesalahan steady state pada sistim proporsional
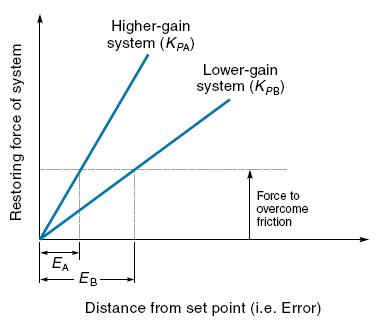
Gambar 1.9. Gain yang lebih besar memiliki error yang lebih kecil
Masalah Gravitasi
Sumber lain dari masalah steady state error adalah masalah gravitasi yang terjadi apabila suatu gaya luar konstan bekerja pada besaran variabel yang dikendalikan. Suatu lengan robot pengangkat beban seperti pada Gambar 1.10. Set point untuk lengan ini adalah 0°, selanjutnya pada saat beban ditambahkan, lengan robot mengalami perubahan posisi. Posisi barunya adalah merupakan posisi dimana gaya pembalik mengimbangi berat yang diberikan yakni sebesar 2 ft. lb. Sistim kendali proporsional hanya dapat gaya pembalik apabila terjadi error dan beban memerlukan suatu gaya konstan untuk mendukungnya. Memperbesar gain dari sistim dapat memperkecil error, namum kendali proporsional sendiri saja tidak dapat menghilangkan masalah ini.
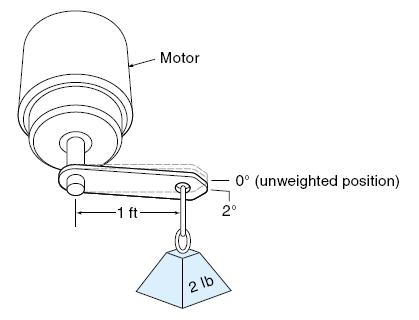
Gambar 1.10. Pembebanan akibat gravitasi menyebabkan lengan bergeser
Contoh 1.3
Tentukan gain KP sistim yang diperlukan untuk menempatkan lengan robot sejauh 5° dari posisi set point (Gambar 1.11). Tahanan total dari gaya gesek dan gravitasi lebih kecil dari 50 in. oz. Motor DC yang digunakan memiliki torsi tetap sebesar 25 in. oz/A dengan rasio sistim roda gigi terpasang adalah 10:1. Satu unit potensiometer feedback dikopel langsung pada poros lengan.
Jawaban / Pemecahan:
Untuk membuat motor turun 5°, maka sistim perlu memberikan torsi pembalik minimal sebesar 50 in. oz pada saat lengan berada pada posisi 5° dari titik set pointnya. Hal ini menentukan kekakuan atau gain (KP) dari sistim dan hal ini ditunjukkan pada Gambar 1.12. Untuk menghitung nilai KP yang diperlukan. Mulai dengan Persamaan 1.1:
![]()
![]()
Sehingga pengendali harus mengatur motor untuk menghasilkan torsi sebesar 10 in. oz untuk setiap derajat gerakan lengan meninggalkan set point. Walaupun begitu, kontroler tidak dapat menggunakan besaran derajat masukan atai kekelauran daya secara langsung – Masukan dan keluaran dari kontroler adalah tegangan (V) dan arus (I) listrik.
Motor sendiri menyediakan torsi sebesar 25 in. oz/A, namun karena menggunakan sistim roda gigi dengan rasio 10:1, maka keluaran torsi dari poros adalah
10 x 25 in. oz/A = 250 in. oz/A
Yang merupakan fungsi transfer steady state motor / sistim roda gigi. Selanjutnya, potensiometer dihubungkan sehingga diperoleh
10 Volt / 350 = 0.029 Volt / deg
Yang merupakan fungsi transfer dari potensiometer. Untuk memperoleh besarnya gain yang diperlukan oleh pengendali, dilakukan perkalian gain sistim dengan fungsi-fungsi transfer:
![]()
Jadi, pengendali harus berfungsi sebagai suatu power amplifier yang memberikan arus 1.38 A ke motor untuk setiap Volt masukan. Untuk menggerakan lengan ke posisi 30° maka akan diberikan tegangan masukan ke motor sebesar:
30° x 0.029 V/deg = 0.87 V
Anggap lengan berada pada 0°, maka sinyal error adalah
0.87 V – 0 V = 0,87 V
Tegangan error sebesar 0.87 V ini akan dikonversi oleh amplifier menjadi
0.87 V x 138 A/V = 1.2A
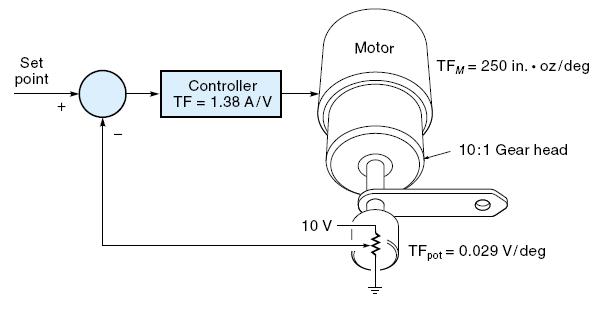
Gambar 1.11. Kontrol Sistim yang dibahas
Nilai awal arus ini akan menggerakan motor dan sistim roda gigi untuk menghasilkan torsi sebesar
250 in. oz/A x 1.2A = 300 in. oz.
Pada akhirnya pada saat mana error mengecil, demikian juga dengan besaran torsi. Bilamana lengan hanya mencapai posisi 25° (masih kurang 5°), torsi mengecil menjadi 50 in. oz (yang berdasarkan rancangan, cukup untuk mengatasi gaya gesek).
132125676 (c) 2012