Sistim Kendali Umpan-Balik

1.5. KENDALI DERIVATIF

Salah satu pemecahan untuk menangani masalah lonjakan adalah dengan menggunakan kendali derivatif. Kendali derivatif merupakan rem yang berfungsi untuk meredam lonjakan variabel yang dikendalikan, memperlambat gerakan variabel yang dikendalikan beberapa saat sebelum mencapai tujuan. Secara Matematis, kontribusi dari kendali derivatif dinyatakan dengan persamaan berikut:

Dimana:

Output = keluaran kendali derivatif
K_D = Konstanta gain derivatif (juga sering ditulis sebagai T_D, satuan adalah waktu)
K_P = Konstanta gain proporsional
ΔE/Δt = tingkat perubahan error (kemiringan kurva error)

Gambar 1.18 menunjukan bagaimana suatu sistim pengendali posisi dengan menggunakan umpan balik derivatif bereaksi terhadap perubahan nilai set point. Secara khusus, Gambar 1.18(a) menunjukan posisi aktual dan posisi yang diinginkan dari variabel yang dikendalikan, Gambar 1.18(b) menunjukan kesalahan (error) dari posisi, dan Gambar 1.18(c) menunjukan keluaran dari sistim kendali. Asumsikan bahwa variabell yang dikendalikan pada awalnya berada pada posisi 0°. Kemudian pada waktu A set point dirubah dengan segera menjadi 30°. Disebabkan oleh inersia mekanik, maka diperlukan waktu untuk benda dapat mencapai kecepatan geraknya. Perhatikan bahwa kesalahan posisi (E) meningkat (kemiringan positif) selama periode waktu A ke B. Dengan demikian, kendali derivatif , yang berbanding lurus dengan kemiringan kurva error, akan memiliki output positif, yang memberikan dorongan kepada benda, agar dapat bergerak. Sebagaimana variabel yang dikendalikan mendekati nilai set point (B ke C), kesalahan posisi berkurang (kemiringan kurva negatif), sehingga kendali derivatif memberikan gaya negatif mirip fungsi rem yang bereaksi untuk memperlambat gerakan benda.

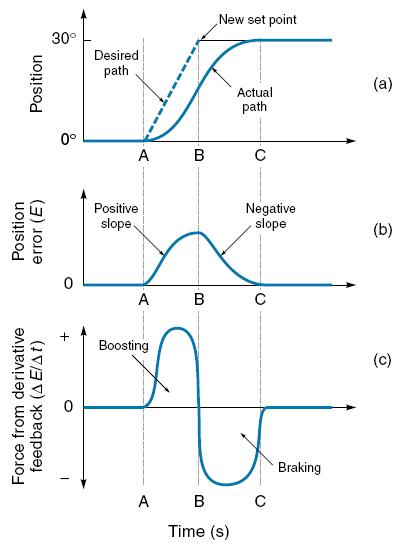Gambar 1.18. Kontribusi kendali derivatif untuk mendorong dan memperlambat

Untuk sistim kendali proses, dimana set point biasanya merupakan suatu nilai tetap, kendali derivatif membantu agar sistim bereaksi lebih cepat terhadap perubahan beban. Sebagai contoh, tinjau sebuah pengendali yang dipergunakan untuk menjaga permukaan cairan agar tetap konstan di dalam tangki. Jika terjadi penurunan level cairan yang cepat (kemiringan positive pada kurva error), maka kendali derivatif bereaksi dengan membuka katup pipa masukan lebih lebar dibandingkan dengan yang dapat dilakukan oleh kendali proporsional. Selanjutnya, apabila level cairan hampir kembali normal pada set point dan error mengecil (kemiringan negatif kurva error, maka kendali derivatif membantu untuk menutup katup seluruhnya.

Dari pembahasan selama ini, kita dapat melihat bahwa kendali derivatif meningkatkan unjuk kerja sistim melalui dua cara. Pertama, kendali jenis ini memberikan dorongan gaya pada awal perubahan untuk memberikan reaksi yang lebih cepat; kedua, kendali jenis ini memberikan kemampuan pengereman apabila objek mendekati titik set point yang baru.

Aksi pengereman ini, tidak hanya membantu untuk mengurangi lonjakan namun juga cenderung mengurangi error steady state.

Secara alamiah, pengaruh dari kendali derivatif pada suatu sistim adalah proporsional terhadap K_D (pada Pers. 1.5); karena umpan balik derivatif meningkatkan respons sistim secara keseluruhan, kita dapat mengira bahwa nilai K_D dapat dibuat sebesar mungkin. Namun, terlalu banyak umpan balik derivatif yang diberikan akan malah memperlambat reaksi sistim dan memperbesar derau (noise). Disini diperlukan suatu perbandingan yang tepat agar diperoleh besaran uimpan balik derivatif yang sesuai. Hal penting yang perlu dicatat adalah bahwa kendali derivatif tidak mempengaruhi akurasi dari sistim, kendali ini hanya meningkatkan waktu respons, sehingga tidak dapat dipergunakan sebagai suatu alternative kendali tunggal pada sistim.

132125676 (c) 2102