Sistim Kendali Umpan-Balik

1.6. KENDALI PROPORSIONAL + INTEGRAL + DERIVATIF

Banyak sistim-sistim kendali menggunakan suatu kombinasi dari ketiga jenis umpan balik yang telah dibahas diatas, yakni kendali Proporsional + Integral + Dertivative. Dasar dari sistim ini adalah kendali proporsional. Dengan menambahkan kendali integral maka diperoleh kemampuan untuk menghilangkan error steady state namun meningkatkan lonjakan pada sistim. Kendali derivatif memberikan kemampuan untuk memperoleh sistim dengan lonjakan yang rendah dan yang bergerak cepat. Respons dari suatu sistim kendali PID dapat dijelaskan dengan menggunakan Persamaan 1.6, yang merupakan suatu persamaan yang menjumlahkan ketiga persamaan sistim kendali tersebut.

                     (1.6)

Bentuk lain dari persaman diatas diperoleh melalui proses faktorisasi KP sehingga diperoleh

                             (1.6a)

Dimana:

Output _PID = Keluaran dari kendali PID
K_P = Gain kendali proporsional
K_I = Gain kendali integral (juga sering ditulis sebagai 1/TI)
K_D = Gain kendali derivatif (juga sering ditulis sebagai TD)
E = Error (deviasi dari set point)
Σ(EΔt) = Jumlah keseluruhan error yang terjadi (daerah dibawah kurva error .waktu)
ΔE/Δt = Tingkat perubahan error (kemiringan kurva error)

Pengendali PID Analog

Pengendali yang mempergunakan persamaan PID (1.16a) dapat dalam bentuk analog maupun digital, namum hampir semua implementasi nyata berbentuk digital. Gambar 1.19 menunjukkan suatu sistim ringkas untuk kendali PID dalam bentuk analog dengan menggunakan lima penguat selisih tegangan. Amplifier selisih tegangan yang pertama (U₁) mengurangkan besarnya nilai feedback dari nilai set point untuk mendapatkan sinyal error. Op-amp U₂, U₃, dan U₄ dikonfigurasikan untuk berfungsi sebagai masing-masing sebagai penguat unit gain, integrator, dan differensiator. Masing-masing menghasilkan besaran-besaran untuk bagian-bagian di dalam kurung pada persamaan PID 1.6a. Penguat akhir (U₅) menjumlahkan ketiga bagian didalam kurung dan mengalikannya dengan K_P untuk menghasilkan output sistim. Kapasitor C_I pada bagian integrator mengakumulasikan error dalam bentuk muatan listrik, dan kapasitor C_D pada bagian differensiator hanya melewatkan muatan listrik yang mewakili perubahan error. Konstanta-konstanta K_P, K_I dan K_D dipilih dengan mengatur masing-masing nilai-nilai R₁, R₂, dan R₃.

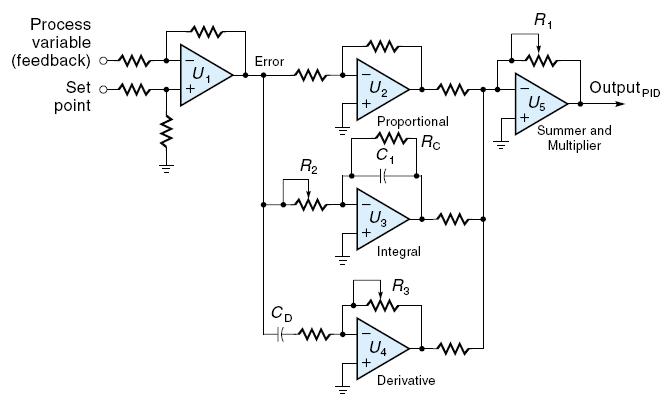
Gambar 1.19. Pengendali PID Analog

Rangkaian pada Gambar 1.19 dapat mengimplementasikan persamaan PID dengan tepat, namun pertimbangan-pertimbangan praktis terkadang membuat gambarannya menjadi lebih kompleks. Sebagai misal, amplifier yang nyata memiliki batas atas dan batas bawah operasi, jika amplifier dikerjakan diluar batas-batas ini, maka kerja amplifier akan menjadi tidak linier lagi. Perubahan sinyal yang besar dan cepat dapat menyebabkan integrator atau differensiator mengalami saturasi. Jika hal ini terjadi, output dari bagian yang mengalami saturasi akan mendominasi keseluruhan output dari pengendali, sehingga menyebabkan sistim menjadi tidak stabil.

Salah satu masalah yang berhubungan dengan integrator adalah kondisi windup. Hal ini terjadi bila sistim mengalami gangguan luar yang besar, sehingga dalam usaha dari pengendali proporsional untuk menangani keadaan ini, mengalami saturasi dan menjadi on sepenuhnya. Disebabkan karena sistim tidak dapat menyediakan output sebanyak yang dibu tuhkan maka keadaan error akan berlangsung lebih lama dari yang diperhitungkan secara teoritis, dan sementara itu integrator melakukan proses akumulasi error. Konsekuensinya, pada saat error akhirnya berkurang, factor akumulasi integral yang tinggi dapat menyebabkan terjadinya overshoot (lonjakan). Salah satu solusi untuk masalah ini adalah dengan memutuskan aliran listrik ke bagian kendali integral apabila sistim mengalami saturasi.

Masalah lain dengan kendali integral adalah bahwa integrator ideal akan menjumlahkan seluruh daerah error dot waktu (sejak dari awal). Dapat ditunjukkan bahwa hasil yang lebih dari sistim jika integrator dapat perlahan-lahan “melupakan” pengaruh error dari waktu yang lama sebelumnya. Hal ini dapat dilakukan dengan membiarkan muatan untuk dapat habis dari kapasitor C_I secara perlahan dengan menggunakan resistor R_C (pada Gambar 1.19).

Suatu masalah yang dapat terjadi pada kendali derivatif adalah hal sebagai berikut: pada sistim kendali yang nyata, set point biasanya dinaikan atau diturunkan dalam langkah-langkah nilai yang tidak kontinyu. Suatu perubahan langkah tidak kontinyu ini memiliki kemiringan kurva yang tidak berhingga, yang akan dapat menyebabkan fungsi derivatif mengalami saturasi. Salah satu pemecahan untuk masalah ini adalah dengan mendasari kendali derivatif hanya dengan menggunakan sinyal feedback (PV) daripada dengan menggunakan sinyal error, dikarenakan variabel yang dikendalikan (apakah itu suhu, posisi atau yang lainnya) sebenarnya tidak dapat berubah dengan tiba-tiba, walaupun untuk set point hal ini mungkin terjadi. Persamaan PID untuk sistim yang telah dimodifikasi adalah sebagai berikut:

                     (1.7)

Dimana:

Output_PID = output pengendali
K_P, K_I, K_D = nilai-nilai gain untuk sistim proporsional, integral dan derivatif
E = error (SP-PV)
PV = variabel proses (umpan balik dari sensor)

Suatu pengendali untuk aplikasi nyata harus dirancang untuk mampu menangani berbagai masalah seperti yang telah didiskusikan diatas, namun biasanya sifat alam dan perluasan modifikasi rancangan yang diperlukan belum diketahui hingga pada saat prototype hardware yang sebenarnya dapat di uji coba.