Sistim Kendali Umpan-Balik

11.4. PENGENDALI INTEGRAL

Penggunaan kendali integral pada sistim kendali dapat mengurangi error steady state menjadi nol. Kendali integral menghasilkan gaya pembalik yang proporsional untuk jumlah dari keseluruhan error dikalikan waktu, seperti yang dinyatakan oleh Persamaan 1.4:

Output I = KI + KP Σ(EΔt)

Dimana:

Output = keluaran pengendali integral
K_I = konstanta kendali integral (juga dinyatakan dalam bentuk 1/T_I)
K_P = konstanta gain proporsional
Σ(EΔt) = jumlah dari keseluruhan error (dikalikan dengan waktu terjadinya).

Untuk suatu nilai error yang konstan, nilai Σ(EΔt) akan meningkat seiring waktu, menyebabkan gaya pembalik semakin membesar. Pada akhirnya gaya pembalik akan menjadi cukup besar untuk mengatasi gaya gesek dan menggerakan variabel yang dikendalikan dalam besaran untuk menghilangkan error yang terjadi.

Hal ini dapat dianalogikan dengan ilustrasi berikut. Seorang yang sedang duduk membaca didalam ruangan yang memiliki wastafel, sementara membaca orang ini menyadari bahwa kran pada wastafel tidak ditutup dengan rapat sehingga ada alir mengalir mrngisi bak wastafel. Dengan berjalannya waktu, orang in tetap meneruskan membaca, hingga suatu saat air memenuhi bak wastafel, pada saat ini orang ini berhenti membaca dan menuju kran wastafel sebelum tumpah keluar dari bak wastafel. Disini laju kebocoran tidak berubah namun efek dari keadaan steady state (jumlah air di bak) terus bertambah seiring waktu hingga akhirnya sistim (pembaca) termotivasi untuk melakukan sesuatu (menutup kran dengan rapat).

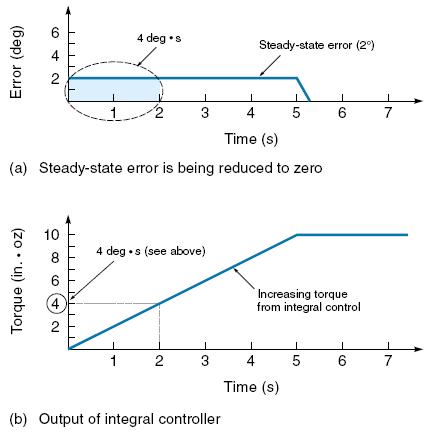
Gambar 1.15. Grafik yang menunjukan kendali integral mengatasi steady state error (K_I K_P = 1)

Contoh 11.4

Tinjau suatu kasus dimana suatu lengan robot memiliki error posisi steady state sebesar 2° disebabkan oleh gesekan; error ini ditunjukkan pada Gambar 1.15(a). Dengan berjalannya waktu, error tetap sebesar 2°. Gambar 1.15(b) menunjukan torsi pembalik yang disebabkan oleh kendali integral yang meningkat seiring waktu. Besarnya torsi pembalik pada sembarang waktu adalah proporsional dengan luas daerah dibawah kurva error. Sebagai contoh, setelah 2 detik luas daerah dibawah kurva adalah 4° .det (luas = 2° x 2 det), seperti yang dilustrasikan pada Gambar 1.15(a). Dengan asumsi bahwa K_P = 1 in.oz/° dan K_I = 1/s, maka K_P/K_I = 1 in.oz/° [Gambar 1.15(b)]. Setelah sekitar 5 detik, gaya pembalik menjadi cukup besar untuk melawan gaya gesek dan mengangkat lengan robot sejauh 2° untuk menghilangkan error yang terjadi. Sekali error menjadi nol, luas daerah dibawah kurva berhenti bertambah, sehingga torsi juga berhenti bertambah; walaupun demikian, lengan tetap berada pada level 10 in.oz. Hal yang terakhir ini sangat penting karena hal ini berguna untuk mengatasi gaya gravitasi, seperti yang ditunjukkan pada Contoh 11.5.

Contoh 11.5

Sistim umpan balik proporsional pada Contoh 1.3 (K_P = 10 in.oz/°) dimodifikasi untuk juga menggunakan sistim umpan balik integral. Lengan berada dalam keadaan diam (pada posisi 30°) pada saat sebuah beban ditambahkan pada ujung lengan, sehingga menyebabkan terjadinya torsi ke arah bawah sebesar 40 in.oz [Gambar 1.16(a)]. Jelaskan bagaimana sistim bereaksi terhadap penambahan beban ini.

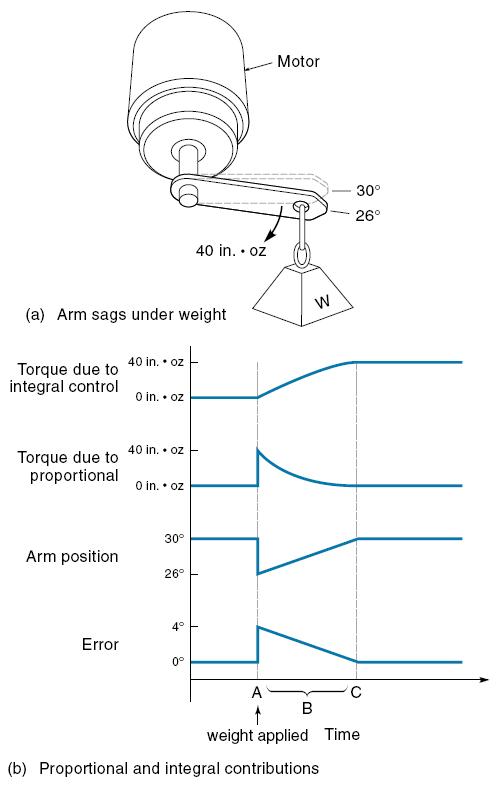
Gambar 1.16.Respons sistim proporsional plus kendali integral

Pemecahan

Gain proporsional dari sistim ditentukan sebesar 10 in.oz/°. Seperti yang ditunjukkan oleh perhitungan berikut, torsi sebesar 40 in.oz akibat adanya beban menyebabkan lengan bergeser sejauh 4°.

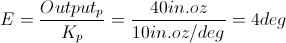
Hal ini ditunjukan dalam waktu A pada Gambar 1.16(b).

Awalnya kendali proporsional menyediakan keseluruhan gaya pembalik 40 in.oz untuk menopang lengan, ini menyebabkan terjadinya error sebesar 4°. Dikeranakan adanya error, maka kendali integral memberikan kontribusinya untuk gaya pembalik. Dengan berjalannya waktu, luas daerah dibawah kurva error bertambah luas, dan kendali integral menyediakan lebih banyak gaya sebesar 40 in.oz. Sebaliknya kontribusi sistim proporsional untuk gaya 40 in.oz berangsur-angsur berkurang [ditunjukkan sebagai waktu B dalam Gambar 1.16(b)]. Pada akhrnya pada waktu C, kendali integral telah memberikan kontribusi yang menyeluruh untuk gaya pembalik 40 in.oz dan error menjadi 0. Suatu keadaan steady state yang baru kembali tercapai.

Respons kendali integral dengan mudah dapat diobservasi pada unit-unit robot yang digunakan di industri. Pada saat beban diletakkan, lengan akan turun sebentar kemudian naik lagi ke posisi semula. Konstanta integral K_I secara umum dinotasikan sebagai 1/T mengacu kepada “perulangan per menit” (atau “perulangan per detik”). Hal ini dikarenakan (jika K_I=1), maka kontribusi integral akan bertambah sebanyak kontribusi proporsional setiap perioda waktu. Jika K_I = 2, maka kontribusi integral akam bertambah sebesar dua kali banyaknya kontribusi proporsional setiap perioda waktu. Hal ini dapat dilihat pada Gambar 1.15(a). Ingat kembali bahwa bila K_P = 1 dan K_I = 1 dan steady state error sebesar 2° [seperti yang ditunjukan pada Gambar 1.15(a). Dengan demikian kontribusi dari  Kendali proporsional sendiri akan sebesar 2 in.oz (K_PE = 1 x 2 = 2). Sekarang tinjau Gambar 1.15(b) dan perhatikan bahwa kontribusi juga meningkat dengan jumlah yang sama sebesar 2 in.oz disetiap periode waktu.

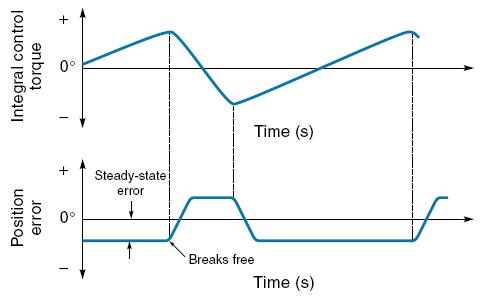
Gambar 1.17. Kendali integral dapat menyebabkan lonjakan dan osilasi

Walaupun penambahan umpan balik integral menghilangkan masalah steady state error, namun hal ini mengurangi kestabilan sistim. Masalah muncul disebabkan umpan balik integral cenderung membuat sistim mengalami lonjakan (overshoot), yang dapat mengarah ke osilasi. Salah satu contoh ditunjukkan melalui grafik pada Gambar 1.17. Semua sistim-sistim mekanik mengalami gaya gesek, dan gaya ini bersifat tidak linier – artinya diperlukan gaya yang lebih besar untuk melawan gaya gesek pada saat objek berada dalam keadaan diam daripada yang dibutuhkan untuk mempertahankan benda untuk tetap bergerak. Pada saat waktu t = 0, sistim pada Gambar 1.17 baru bergerak dan berhenti pada posisi yang baru, menghasilkan suatu keadaan steady state error. Gaya pembalik setara dengan kontribusi dari kendali proposional ditambah peningkatan gaya dari kendali integral. Untuk beberapa saat benda tidak bergerak, namun akhirnya oleh karena kombinasi gaya pembalik yang dapat mengatasi gesekan maka benda bergerak. Sekali benda telah bergerak, gaya yang diperlukan berkurang, sehingga terdapat kelebihan gaya dorong, yang terpakai untuk mempercepat benda. Hal ini dapat menyebabkan terjadinya lonjakan (overshoot) sebelum suatu proses pengereman dapat dilakukan. Jadi, walaupun penambahan umpan balik integral menyelesaikan satu masalah yakni steady state error, namun masalah lainnya muncul: yakni lonjakan dan berkurangnya stabilitas dari sistim. Selain itu, respons dari umpan balik integral relative lambat karena diperlukan waktu beberapa saat untuk error x waktu untuk mencapai besaran tertentu.

132125676 (c) 2012